Faz 150 anos que os epidemiologistas calculam desfechos – às vezes sombrios – para o espalhamento de doenças. O objetivo não é espalhar terror: é evitar que as previsões se concretizem. Entenda de uma vez por todas por que os negacionistas do isolamento estão falando besteira.
Texto: Maria Clara Rossini | Ilustração: Lasca Studio | Design: Carlos Eduardo Hara | Edição: Bruno Vaiano
No verão de 1854, ao longo de três dias, 127 pessoas morreram de cólera em uma única rua do bairro do Soho, no centro de Londres. A doença causa diarreia, desidratação e hemorragia. Sem tratamento, até metade dos infectados sucumbe em algumas horas. As autoridades da época tinham certeza absoluta de que a cólera era transmitida pelo ar. Mas o médico John Snow (não, não é o herói de Game of Thrones) achou estranho. Com o passar dos dias, Snow notou que um único distrito concentrava mais da metade das mortes. Era de se esperar uma distribuição mais homogênea pela cidade, caso a transmissão ocorresse por via aérea. E havia outro mistério: nenhum dos 80 funcionários de uma fábrica de cerveja localizada no epicentro da epidemia adoeceu.
Intrigado, Snow marcou pontinhos em um mapa, um para cada vítima, e notou que todas moravam em torno de uma única bomba de água (na época, não havia uma torneira em cada casa; as pessoas compartilhavam uma espécie de torneira coletiva). Ele descobriu também que o cano que levava até aquela bomba passava perto de uma fossa. Bingo: a fralda de um bebê com cólera foi descartada na fossa, e uma rachadura no cano permitiu que o cocô contaminasse a água. Por fim, a sacada de Sherlock Holmes: os empregados da cervejaria bebiam tanta cerveja que nem consumiam água. Por isso, ficaram bem.
Foi a primeira vez que alguém deduziu como uma doença é transmitida usando raciocínio lógico, sem conhecer o micróbio responsável. A bactéria causadora da cólera, curiosamente, foi descoberta no mesmo ano, a muitos quilômetros de distância, pelo anatomista italiano Filippo Pacini. Ninguém deu bola para ele. Hoje, John Snow é considerado o pai da epidemiologia – de quebra, ganhou um bar em sua homenagem em Londres. Qualquer pessoa chamada John Snow bebe de graça por lá; basta mostrar um documento. Afinal, em caso de cólera, cerveja é a aposta mais segura (rs).
Desde então, a matemática prestou serviços cada vez mais valiosos à saúde pública. No início do século 20, o médico Ronald Ross descobriu que a malária era transmitida por um vetor, os mosquitos do gênero Anopheles. Em 1910, ele propôs a seguinte reflexão: se colocarmos um único indivíduo com malária e um único mosquito Anopheles em uma população livre da doença, quais são as chances do mosquito picar o doente e então transmitir a doença, por meio de outra picada, para alguém saudável?
Esse experimento mental deu origem ao parâmetro R0 (“erre-zero”): quanta gente uma única pessoa contaminada é capaz de infectar, em média. O R0 do sarampo, por exemplo, é altíssimo: um único infectado pode deixar de 12 a 18 pessoas doentes. Com base em parâmetros como o R0, é possível construir equações que descrevem como uma epidemia se espalha (ou seja: automatizar o trabalho que John Snow realizou com um lápis e um mapa).
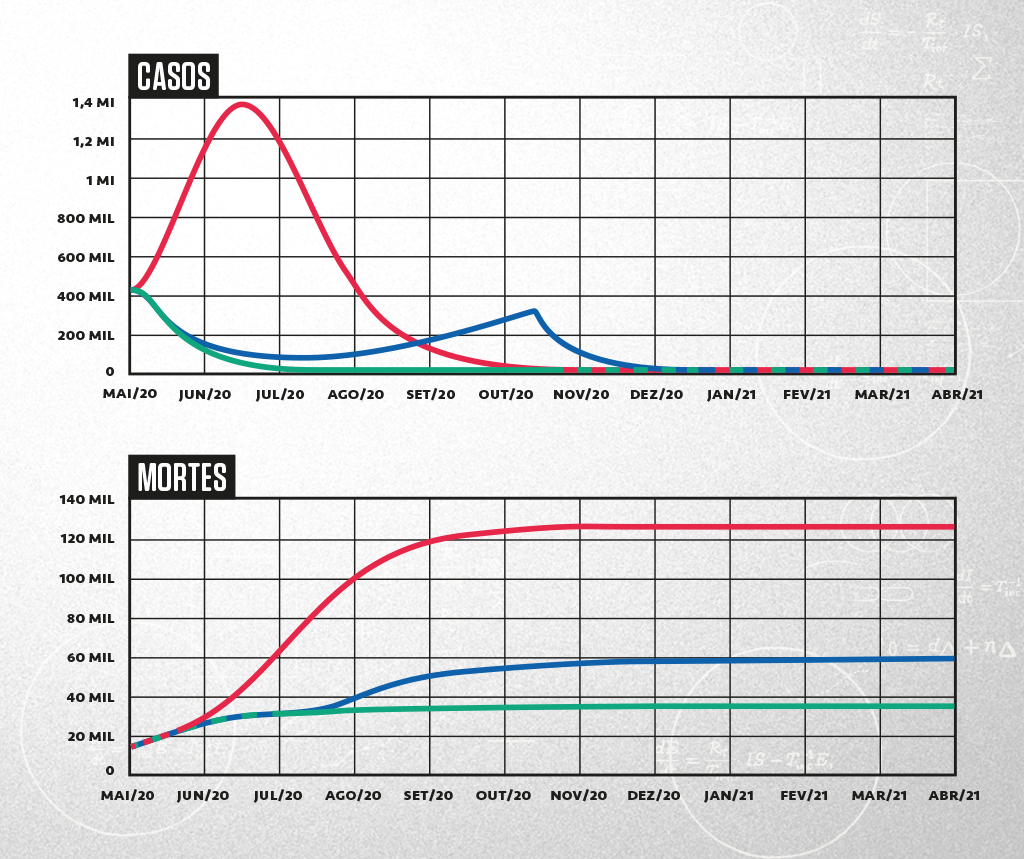
Hoje, existem modelos epidemiológicos para tudo que você imaginar. Há alguns que preveem as mutações e a sazonalidade do vírus da dengue. Outros são específicos para vírus que infectam as pessoas para o resto da vida, como o HIV. Há ainda aqueles para bactérias recorrentes, causadoras de infecção alimentar. E agora há modelos específicos para a Covid-19, que geram os gráficos exibidos nos jornais todos os dias. Isso levanta muitas questões: como esses gráficos são gerados? Por que as previsões dão errado com tanta frequência? Por que cada previsão dá um resultado diferente? Vamos respondê-las.