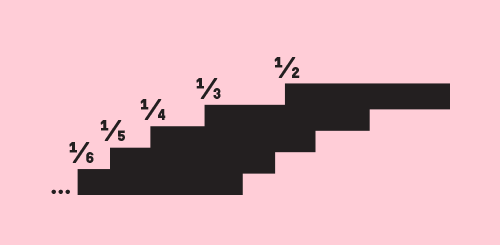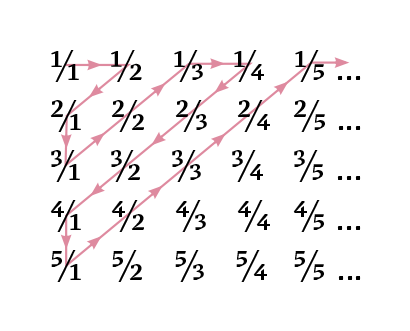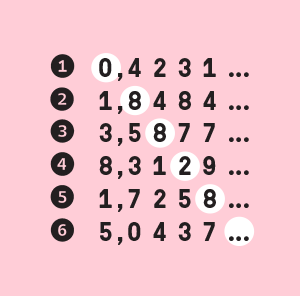Existe alguma coisa maior do que o infinito?

13 jan 2021
18h14

Em 1891, o matemático Georg Cantor provou que alguns infinitos são maiores que outros – e que os maiores infinitos se escondem nos vãos entre os números, e não além deles. Sua descoberta seria eternizada em um conto de fadas sobre um hotel impossível, com um número sem fim de quartos.

^{Texto: Bruno Vaiano | Ilustração: Yann Valber | Design: Carlos Eduardo Hara}

o paraíso do coronavírus: o Grande Hotel Hilbert, um hotel com infinitos quartos, todos ocupados. O recepcionista, satisfeito, põe uma plaquinha em cima do balcão: “Não há vagas”. Eis que, em meio a uma forte chuva, um viajante cruza a porta pedindo abrigo. Estão prestes a recusá-lo quando o zelador – um certo Georg Cantor – diz: “Tudo bem. A gente dá um jeito”.

Continua após a publicidade

Para resolver o impasse, Cantor pede a todos os hóspedes que se mudem um quarto para frente. O do quarto 1 vai para o quarto 2. O do quarto 2, para o quarto 3… Isso libera o primeiro quarto para o viajante, sem desalojar ninguém que já estava lá. Fosse este um hotel comum, o cliente do último quarto não teria para onde ir. Mas o hotel é infinito. Não existe último quarto; sempre há um depois.

Então chega um ônibus de excursão infinito, lotado com infinitos aposentados. Cantor tem uma ideia: passar todos os hóspedes para quartos pares. A pessoa do quarto 1 vai para o quarto 2. A do quarto 2, para o quarto 4. A do quarto 3, para o quarto 6. O procedimento libera a totalidade dos quartos ímpares, que também são infinitos. E assim Cantor acomoda todos os velhinhos.

Em qualquer sequência de números consecutivos, metade deles serão pares e metade, ímpares. Como hóspedes vão caber em metade dos quartos em que cabiam antes? Bem, metade do infinito é infinito. E o dobro também. No Grande Hotel Hilbert, “metade” e “dobro” não existem. De fato, infinito vezes infinito também dá infinito: mesmo infinitos ônibus com infinitos hóspedes caberiam no hotel.

Continua após a publicidade

Na vida real, Cantor não foi zelador. Foi um matemático alemão do final do século 19. E a historinha do hotel não é um devaneio da Super: era a maneira como outro matemático, o inglês David Hilbert, explicava o trabalho de Cantor em palestras. Daí “Grande Hotel Hilbert”.

Existe uma maneira de vencer a dinâmica do hotel? Alguma quantidade de pessoas que ele não conseguiria hospedar com nenhum truque engenhoso? Sim, existe. Há dois tipos de infinito: um que cabe no hotel, outro que não. A descoberta do infinito que não cabe foi a grande contribuição de Cantor à matemática. Falaremos dela mais adiante.

O entusiasmo de Hilbert com o trabalho de Cantor foi a exceção, não a regra. Os matemáticos da época não eram cabeça aberta o suficiente para aceitar conclusões tão contraintuitivas. Henri Poincaré disse que as ideias de Cantor eram “uma enfermidade, uma doença perversa da qual os matemáticos, algum dia, hão de ser curados”. Leopold Kronecker, um ex-professor de Cantor, chamou-o de “charlatão” e “corruptor da juventude”. Ele apanhou tanto que teve um colapso nervoso aos 39 anos, em 1884. Passou o resto da vida sufocado por uma depressão profunda e morreu internado em um hospital psiquiátrico.

Séries infinitas

ara entender o drama, precisamos dar alguns passos atrás na história. Cantor não foi a primeira vítima da intolerância ao infinito. Diz a lenda: quando Hipaso, um dos pupilos de Pitágoras, mostrou ao mestre e aos colegas que a raiz quadrada de dois (√2) é um número irracional – cujas casas decimais continuam para sempre e não seguem nenhum padrão –, ele foi lançado ao Mar Mediterrâneo com um peso amarrado aos pés.

A contemplação do infinito pelo ser humano começa aproximadamente 500 anos antes de Cristo com uma lista de paradoxos propostos pelo grego Zeno de Eleia, que chegou até nós indiretamente pelos escritos de Aristóteles. Um deles, o paradoxo da dicotomia, diz o seguinte: para uma pessoa percorrer uma distância de 2 m, ela precisa antes percorrer metade disso, que dá 1 m. Mas para percorrer m, ela precisa percorrer metade, que dá 0,5 m. Para percorrer 0,5 m, ela precisa percorrer metade, que dá 0,25 m…

De fato, para percorrer qualquer distância é preciso primeiro vencer a metade dessa distância. Como toda distância tem uma metade, todo deslocamento entre um ponto A e um ponto B envolve completar um número infinito de tarefas. Esse é o paradoxo: embora seja impossível completar infinitas tarefas em um tempo finito, sabemos do cotidiano que qualquer um consegue andar do ponto A ao ponto B.

Esse é um exemplo daquilo que os matemáticos batizaram mais tarde como série convergente. Nesse caso, temos uma soma de infinitas frações (meio, quarto, oitavo, sempre a metade da metade) que ficam cada vez menores: 1 + ½ + ¼ + 1/8… Mas o resultado dessa soma é uma distância finita e banal: 2. Daí o nome “convergente”: uma série com infinitos termos que converge em um valor finito.

Perceba que, quanto mais termos você adiciona na soma, mais você se aproxima do 2, mas ele é um limite inalcançável – como a cenoura pendurada na vara de pescar, que o burrinho tenta morder e não consegue. 1 + 0,5 dá 1,5. Adicione 0,25 e temos 1,75. Adicione 0,125 e temos 1,875.

Continua após a publicidade

Converge ou diverge?
“Séries” são somas de infinitos termos. Algumas dessas somas são convergentes: o resultado se aproxima de um número chamado limite, sem jamais alcançá-lo. Outras são divergentes e dão um resultado infinito. Conheça um exemplo de cada.

1. A série harmônica
Até onde dá para empilhar livros em uma mesa de modo que eles avancem além da beirada? Infinitamente. Basta o primeiro livro ficar metade para fora. O segundo, um terço… E assim por diante.

–

Essa é a série harmônica (½ + ⅓ + ¼…). Ela é divergente. Embora as frações fiquem cada vez menores, o resultado da soma é infinito. Com infinitos livros, a pilha se estenderia infinitamente além da beirada.

Continua após a publicidade

2. O paradoxo da dicotomia
Uma famosa série convergente está contida em um dos paradoxos do grego Zeno. A ideia é que, para andar uma distância – digamos, 2 m –, você precisa andar metade dela (1 m). E para andar metade, você precisa andar um quarto (0,5 m). E para andar um quarto… Isso é representado pela soma: 1 + ½ + ¼ + ⅛ + … = 2.

Na vida real, é fácil percorrer 2 m. Mas, no papel, é impossível realizar uma soma infinita. Podemos só nos aproximar somando cada vez mais frações. Eis uma série convergente. A soma das quatro primeiras frações dá 1,875. Das seis primeiras, 1,968. Das oito primeiras, 1,971. A soma de infinitas frações dará precisamente 2.

Diferentes, mas iguais

utra grande contribuição ao estudo do infinito vem na forma de um paradoxo contido no último livro de Galileu Galilei, Duas Novas Ciências, publicado em 1638. Galileu começa com a constatação básica de que todo número pode ser elevado ao quadrado – ou seja, multiplicado por si mesmo. Como os números naturais (1, 2, 3…) são infinitos, então também existem infinitos quadrados.

1² = 1

2² = 4

Continua após a publicidade

3² = 9

Nossa intuição diz que os quadrados formam um grupo menor que os números naturais. Mas se todo número tem o seu quadrado, então precisam existir infinitos quadrados também. É como se existissem menos cachorros do que donos, mas mesmo assim cada dono tivesse um cachorro só para si. Como pode dois grupos serem infinitos se um é maior que o outro?

250 anos depois, Cantor reformulou a ideia de Galileu em termos de conjuntos. A palavra está sendo usada na acepção mais óbvia possível: uma coleção de itens, como quatro cachorros no quintal, cinco bananas na fruteira etc. Cantor chamou a quantidade de elementos de um conjunto de cardinalidade.

Continua após a publicidade

Pegue um conjunto com cinco crianças e outro com as cinco mães dessas crianças. Cada criança tem uma mãe, o que significa que os dois conjuntos podem ser pareados. A noção de pareamento é importante por causa do seguinte: quando nós contamos alguma coisa – tipo o número de cães em um quintal – estamos fazendo o equivalente a parear o conjunto de cães com o conjunto dos números naturais. Você atribui o número 1 ao vira-lata caramelo, o número 2 ao pitbull, o número 3 ao chihuahua…

Você poderia parear para sempre, caso houvesse infinitos cães, porque o conjunto dos números naturais tem cardinalidade infinita: 1, 2, 3, 4, 5, 6… Cantor chamou essa cardinalidade infinita de alef zero (“alef” é a primeira letra do alfabeto hebraico – e é só um nome. Poderia chamar Jairo, mas Cantor deu um toque mítico).

O ponto é: se você tem um conjunto infinito qualquer em mãos e ele pode ser pareado com os naturais – ou seja, se os cachorros podem ser contados em princípio, ignorando o fato de que a contagem continua para sempre –, então a cardinalidade desse conjunto será a mesma dos naturais: alef zero. Serão infinitos do mesmo tamanho, mesmo que não pareçam.

Continua após a publicidade

Esse é o processo de pensamento do zelador do Grande Hotel Hilbert: ele sabe que, enquanto puder atribuir um número específico a cada hóspede recém-chegado – ou seja, enquanto puder contar, ainda que seja impossível contar até o infinito –, haverá vagas. Pois qualquer conjunto infinito contável tem a mesma cardinalidade alef zero, que é a capacidade do hotel. E assim surge a armadilha: existe algum conjunto infinito que não pode ser contado? Cuja cardinalidade é maior que alef zero?

O arranha-céu

única maneira de responder a essa pergunta é escalar o Everest da matemática em busca de conjuntos imensos – na ilustração ao final desta seção, há um mapa para ajudar.

Do mesmo jeito que o conjunto dos quadrados perfeitos (1, 4, 9…) está dentro do conjunto dos números naturais (1, 2, 3…), o conjunto dos naturais está dentro de um conjunto maior, o dos números inteiros – que além dos positivos inclui também o zero e os números negativos. Mas esses dois infinitos, de maneira decepcionante, têm a mesma cardinalidade e podem ser pareados elemento por elemento – mesmo que um pareça, em princípio, o dobro do outro. É só intercalar positivos e negativos:

– (Carlos Eduardo Hara/Superinteressante)

Vamos precisar de algo maior que os inteiros. Tem? Tem. O conjunto dos números racionais, que inclui os números com vírgula. Não quaisquer números com vírgula: só aqueles que a gente consegue obter por meio de frações, que são divisões entre dois números inteiros. Tipo 0,5, que é o resultado da fração ½ . Ou 0,25, que é ¼. O nome “racional” vem do fato de que a palavra “razão” pode ser usada como um sinônimo de “divisão”.

Será que dá para enumerar todas as frações que existem e declarar que elas também são alef zero? Acredite: dá. É só fazer uma tabela infinita com todas as frações, como a que você vê a seguir, e então percorrê-la cortando as diagonais (percorrer uma linha de cada vez não rola, porque a primeira linha nunca terminaria para você passar para a próxima).

Hora de subir mais um andar. Existem números com vírgula que não podem ser expressos por frações? Com certeza. É o caso do terror de Pitágoras, a raiz de dois, que segue para sempre: 1,41421356237… Não existe nenhum número dividido por outro número que dê raiz de dois.

Como não há uma razão (ou seja, uma fração) para representá-la, ela é chamada de número irracional. A raiz de dois é um número irracional razoavelmente bonzinho, diga-se, já que ele pode ser obtido por meio da resolução de uma equação. Existem muitas equações (no Ensino Médio, inclusive) em que o “x” misterioso é a raiz de dois.

A porca só torceu o rabo mesmo quando Cantor percebeu que a maior parte dos números com casas decimais infinitas jamais vão surgir como resultado de uma equação. Estão fora do alcance tanto das frações quanto das incógnitas comuns. Esses monstrinhos receberam o nome de números transcendentais. Nesse caso não se trata apenas de um nome. Eles transcendem mesmo a imaginação e, juntos, formam o equivalente matemático de um deserto inóspito – mais vasto que todo o terreno percorrido até aqui.

Além da muralha

número transcendental mais famoso é o π (pi), que podemos obter apenas por aproximação. 3,14159265359… os matemáticos calculam cada vez mais casas decimais, mas nunca vão chegar ao final: já se conhecem 31 trilhões de dígitos, e eles não seguem nenhuma lógica detectável. Aqui, voltamos às séries infinitas do grego Zeno, porque um dos poucos jeitos de se obter números transcendentais é justamente usar uma série infinita. Leibniz, por exemplo, calculou o π usando essa aqui:

1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11… = π/4

Continua após a publicidade

O π recebe tanta atenção porque é uma exceção: um número transcendental que é útil para nós, essencial para a geometria de círculos ou esferas. π está oculto em tudo que é redondo. E quanto aos demais transcendentais?

Um número transcendental qualquer tem infinitas casas decimais depois da vírgula – e qualquer casa pode ser ocupada aleatoriamente por qualquer dígito de um a nove, sem padrão algum. Isso significa que existem infinitas combinações possíveis. Infinitos números transcendentais como o π, cada um com uma sequência única e infinita de dígitos. Como esses números têm casas decimais infinitas, eles podem ser infinitamente pequenos. Do mesmo jeito que não existe um maior número de todos, não existe um menor número de todos.

Imagine a linha de todos os números formada por vários cones, espaçados de metro em metro, distribuídos ao longo de um deserto. O primeiro cone representa o 1, o segundo, o 2 e assim por diante. Entre esses cones, colocamos no chão pequenos papéis com as frações – os números racionais, como 0,5 ou 0,25. Nessa metáfora, os transcendentais são como a areia: um pó fino que preenche uniformemente os vãos entre os números. Trata-se de uma areia especialmente fina – uma areia infinitamente fina –, pois entre quaisquer dois números, não importa o quão pequenos eles sejam, ainda caberão infinitos grãos, um para cada número transcendental. Um pedaço qualquer do infinito é igualmente infinito.

Continua após a publicidade

Assim Cantor chegou ao fim de sua busca. Esse é um infinito incontável, que não cabe no Grande Hotel Hilbert: não importa o quão engenhoso seja seu método para listar os transcendentais, sempre há como gerar um novo transcendental que não está na lista, o que sempre frustrará a tentativa de contagem. E sem alguma contagem não há como liberar novos quartos. Nós descrevemos esse método no box abaixo. É a prova por diagonalização de Cantor, uma das mais belas e simples da matemática.

A prova do continuum
É impossível listar todos os números com vírgula (os decimais): você sempre acabará deixando infinitos números de fora, mesmo que já tenha contado infinitos deles. Cantor provou isso de uma maneira elegante, que explicamos a seguir.

Continua após a publicidade

1. Existe uma quantidade infinita de números decimais. Escolha alguns aleatórios, como fizemos na tabela abaixo. Essa lista continuará infinitamente tanto para baixo quanto para o lado (pois eles podem ter infinitos dígitos).

2. Agora corte essa lista na diagonal: pegue o primeiro dígito do primeiro número, o segundo dígito do segundo número, o terceiro dígito do terceiro número e assim por diante. representamos esse procedimento com as bolinhas brancas.

–

Continua após a publicidade

3. Monte um novo número usando essa seleção. E agora some um a todos os dígitos desse número. Você obterá um número novo, que não está na sua lista. Sabemos que não está porque ele tem pelo menos um dígito diferente de todos os outros números que estão lá.

: –

4. Mas eu não posso adicionar esse número na lista? Pode. Mas aí bastaria repetir o processo para encontrar um outro número que não está lá. A diagonalização ocorre para sempre. E temos
aí mais uma face do infinito.

Continua após a publicidade

O que Cantor está dizendo é que a linha dos números não é como uma escada com degraus – com distâncias fixas separando o 1 do 2, o 2 do 3, o 3 do 4. Ela na verdade é uma rampa. A linha dos números é um contínuo, em que cada número se dissolve no seguinte, num degradê de infinitos números menores. De fato, Cantor chamou de continuum esse infinito maior que o infinito comum.

Irônico é que, apenas alguns anos depois, também na Alemanha, o físico Max Planck se deu conta de que a natureza não é bem um continuum. No nível microscópico, a realidade é como uma foto: fica pixelada. Quando os físicos lidam com quantidades minúsculas de energia, elas vêm em pacotinhos de tamanho fixo, que não podem ser subdivididos. O menor intervalo de tamanho que as equações da física atual conseguem sondar equivale a 0,000000000000000000000000000000016 cm. É o chamado comprimento de Planck. Beleza: são 33 casas decimais, mas não são infinitas. Ninguém sabe se o próximo avanço teórico irá além desse limite ou se ele é intransponível.

Por muito tempo, os físicos pensaram que o mundo real fosse contínuo, enquanto os matemáticos sequer suspeitavam dos incontáveis grãos de areia que se escondiam debaixo de seus narizes. No fim, calhou que era o contrário: graças a Planck, hoje sabemos que, no nível das menores partículas, a natureza salta degraus. Já Cantor vislumbrou, com sua imaginação, esse domínio minúsculo, liliputiano, que nem nossas melhores equações conseguem acessar. “Do paraíso que Cantor criou, ninguém poderá nos expulsar”, escreveu Hilbert. De fato: o Universo pode até ser infinitamente grande. Mas ele não é maior que os números entre os milímetros de uma régua escolar. O infinito cabe em todos nós.

Tags Relacionadas

Matemática