Conhecimento dos limites
Por que é importante ¿ e não tão difícil ¿ aprender cálculo diferencial.
Luiz Barco
Minha vida de conferencista tem me dado oportunidades gloriosas. Recentemente, convidado no 7o Congresso Brasileiro de Adolescência, em Gramado, Rio Grande do Sul, tive muitas conversas produtivas, além de agradáveis, com jovens da região. Pude perceber que aqueles adolescentes – como provavelmente muitos outros – têm uma visão idealizada da universidade. Talvez seja até por isso que alguns se decepcionam tanto ao chegar lá.
No último encontro, um dos garotos chegou a fazer uma declaração temerária: “Professor, meu irmão estudou Engenharia e um dia desses ele e alguns colegas, também engenheiros, comentaram que nunca usavam alguns tópicos do cálculo diferencial, como os limites, por exemplo. Eles não são importantes?”
Claro que são, apressei-me em responder. Algumas das ferramentas mais usadas no cálculo, como as derivadas e as integrais, são limites especiais. Para tornar a compreensão mais simples, não resisti e tentei mostrar à turma de estudantes o que é o limite para o qual converge uma seqüência n + 1 / n
Logo todos perceberam que para qualquer valor de n ? 0 teremos n + 1 / n ? 1.
E, quanto maior o valor dado a n, mais próximo de 1 fica o limite da seqüência. Experimente você mesmo. Para n = 3, teremos 4/3; para n = 7, 8/7; para n = 100 000, 100 001/100 000.
O caso do 100 000 foi fatal! “Puxa, é praticamente 1! Já pensaram quando n valer um gugol?”, disse uma garota, leitora da SUPER. Poucos entenderam. Com ar superior e certa cumplicidade ela se dirigiu a mim: “Explica pra eles, professor!”
Bom, você, que também é leitor da SUPER, deve saber: gugol é o número formado pelo algarismo 1 seguido de 100 zeros, 10100. Para que você tenha uma idéia de como é grande, saiba que o astrônomo inglês Sir Arthur Stanley Eddington (1882-1944), usando entre outras teorias a física de Einstein, estimou que o número de elétrons em todo o Universo é algo como 1079.
Voltando ao problema proposto pela garota, 1 (+ 99 zeros) 1 / 1 (+ 100 zeros) ficará mais próximo ainda do 1.
Note que n + 1 / = 1 + 1 / n
Repare na tabela:
Para n =
a expressão vale
10……………1,1
100…………..1,01
1000………….1,001
“
“
10 (100)………..1,(99 zeros)1
“Como poderíamos ler esse número?”, eu perguntei. “Diga que é 1 mais um tiquinho de nada”, falou um rapaz. Gostei. De agora em diante, quando falar para crianças, direi que 1 + 1 / n
é praticamente 1, pois quando o n fica bem grandão o 1/n fica um tiquinho de nada.
Para o garoto que falou do irmão engenheiro, expliquei que o Universo e tudo o que há nele está em movimento e que a melhor maneira de descrevermos esses movimentos ainda é nosso velho e bom cálculo diferencial.
Por fim, decidi fazer uma brincadeira que aprendi com Márcio, um pós-graduando de Física na Universidade de São Paulo (USP). É assim: se tempo é dinheiro (T = D) e saber é poder (S = P), logo
D x S = T x P e, conseqüentemente, D = T x P / S
Ora, se passarmos para o limite, concluiremos que quando o saber (S) tende a zero T x P / S tende ao infinito.
Ou seja, se queremos que nosso dinheiro cresça sempre, devemos procurar saber cada vez menos. Parece ser uma grande verdade, mas não é. Mesmo que fosse, dinheiro sem felicidade pouco vale. E só é feliz quem sabe das coisas.
Que perigo são os ditos populares quando tomados ao pé da letra…
Luiz Barco é professor da Escola de Comunicações e Artes da Universidade de São Paulo

 SEGUIR
SEGUIR
 SEGUINDO
SEGUINDO

 Orcas são filmadas oferecendo peixes a humanos. É presente ou manipulação?
Orcas são filmadas oferecendo peixes a humanos. É presente ou manipulação?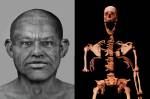 Pela primeira vez, cientistas sequenciam genoma completo de uma pessoa do Egito Antigo
Pela primeira vez, cientistas sequenciam genoma completo de uma pessoa do Egito Antigo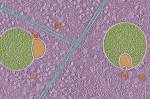 Cientistas descobrem parte nunca antes vista das células humanas
Cientistas descobrem parte nunca antes vista das células humanas Um santo pode perder o título?
Um santo pode perder o título? Quais eram os cheiros na Roma antiga? Acredite, bem ruins
Quais eram os cheiros na Roma antiga? Acredite, bem ruins








