Oráculo
Por aquele cara de Delfos
SEGUIR
SEGUINDO
O que é a fita de Möbius?
Você já deve ter visto essa forma por aí. Mas sabe o que ela significa?
Pergunta enviada por Luiz Fornazari Neto (Irati/PR)
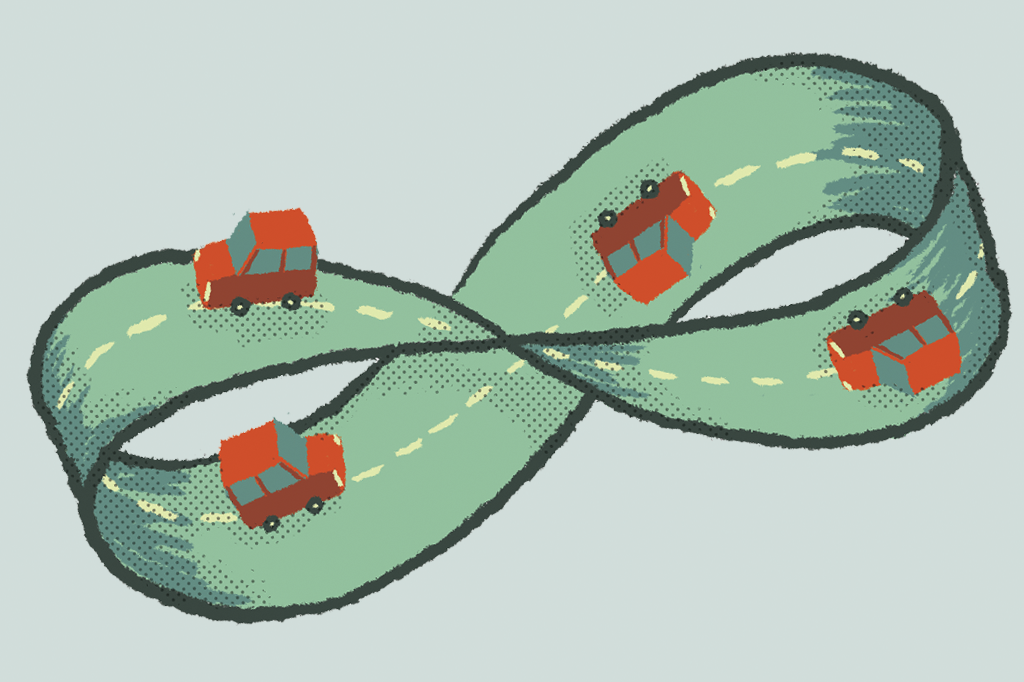
As superfícies convencionais são orientáveis – isto é, têm dois lados. O lado de cima e o lado de baixo de um lençol, por exemplo. Pense numa formiga andando no lençol. Se ela não passar pela borda do lençol, ela não muda de lado. A fita de Möbius, por outro lado, não tem lado. Essa estranha forma, que foi proposta em 1858 pelos matemáticos alemães Johann Listing e August Möbius (daí o nome) é o que o jargão matemático chama de superfície “não orientável”.
Por isso, ela tem propriedades diferentes. Um carro que está andando de um lado da fita é capaz de chegar ao outro lado sem passar pela borda (se você duvida, passe o dedo pela ilustração acima).
A SUPER agradece a professora Christina Brech, da USP, pela explicação.
ACESSO LIVRE COM VIVO FIBRA