Oráculo

Por aquele cara de Delfos

Ser supremo detentor de toda a sabedoria. Envie sua pergunta pelo inbox do Instagram ou para o e-mail maria.costa@abril.com.br.

Ciência

Quem é o Bhaskara da fórmula matemática?

Um importante matemático indiano – que não usava a fórmula que você decorou no Ensino Médio.

Por Luisa Costa
20 abr 2023, 09h32 •

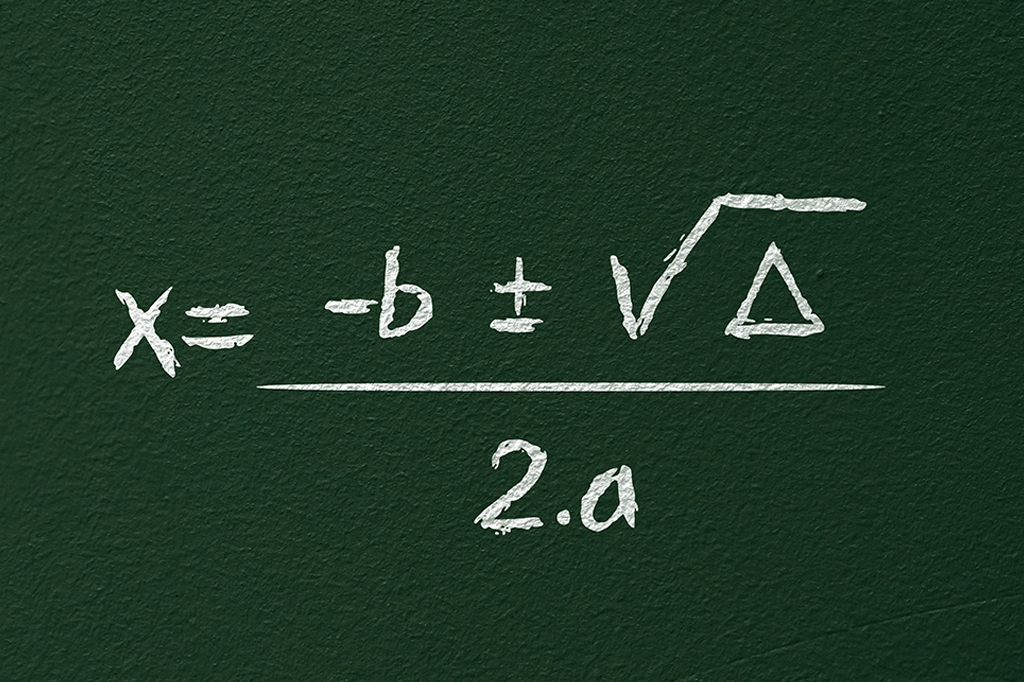
Fotografia da Fórmula de Bhaskara escrita com giz em um quadro. — (Isaac Matos/Getty Images)

A coisa se chama fórmula de Bhaskara apenas no Brasil. E faz pouco sentido: o matemático indiano Bhaskara Akaria não inventou a fórmula.

Conhecido como “o sábio”, Bhaskara nasceu na Índia em 1114 e morreu por volta de 1185. Foi professor, astrólogo, astrônomo – e um dos matemáticos mais importantes do século 12. Sucedeu outro matemático indiano notável, Brahmagupta (598–665), chefiando um observatório astronômico em Ujjain, o principal centro matemático da Índia antiga. Mas não teve relação com a fórmula que leva seu nome.

A fórmula de Bhaskara, para quem não lembra das aulas de Ensino Médio, é: x = -b ± √(b² – 4ac)/ 2a, e ela serve para resolver equações de segundo grau (as do tipo ax² + bx + c = 0).

Até o fim do século 16, não se usava uma fórmula para descobrir os valores de “x” nas equações. Foi a partir dos trabalhos dos matemáticos franceses François Viète e René Descartes, nos séculos 16 e 17, que se tornou comum usar letras para representar os coeficientes de uma equação – e que a resolução geral das equações de segundo grau adquiriu o aspecto que tem hoje.

Na época de Bhaskara, era diferente: os matemáticos usavam “regras”, descrições por extenso, com versos que facilitavam a memorização do passo a passo para resolver equações e outros problemas. Em suas obras, Bhaskara usa regras assim – e cita procedimentos usados por outros matemáticos indianos, como Sridhara, que viveu um século antes dele, para resolver as equações de segundo grau.

Continua após a publicidade

A ideia de dar a Bhaskara os créditos para a fórmula se estabeleceu no Brasil por volta da década de 1960 – e não se sabe ao certo por quê. Uma hipótese está na utilização de um livro do indiano no sistema de ensino brasileiro.

Pergunta de @marciomcpiaui, via Instagram.

Fontes: “Uma breve história da equação do 2º grau”, de Hermes Antônio Pedroso; “A equação quadrática e as contribuições de Bhaskara”, de Eduardo Gomes Guedes; “A fórmula é de Bhaskara?”, na Revista do Professor de Matemática.