Sudoku: a história e a lógica por trás do puzzle mais popular do mundo
Ele foi inspirado em um problema matemático do século 18. Nos anos 2000, virou febre, ganhou seu próprio campeonato mundial e contribuiu para avanços na computação.
O sudoku não veio do Japão. Foi um arquiteto de Indianápolis, nos EUA, que criou o passatempo. Howard Garns tinha 74 anos quando seu jogo foi publicado pela primeira vez na revista Dell Pencil Puzzles & Word Games, em maio de 1979. A brincadeira com números começou a ser impressa sob o nome “Number Place” (algo como “posicionar os números”, descrevendo o objetivo do jogo). E foi assim por alguns anos, sem que o puzzle se expandisse para o resto do país.
Mas também dá para dizer que o sudoku veio do Japão. A partir de 1984, o “Number Place” passou a ser publicado por uma editora japonesa chamada Nikoli. Só que por lá ele era chamado “Suuji Wa Dokushin Ni Kagiru” (“Os Números Devem Ser Únicos”), que depois foi abreviado para Su Doku (“número único”).
Um neozelandês chamado Wayne Gould descobriu o jogo durante uma viagem ao Japão em 1997. Ao longo dos seis anos seguintes, ele desenvolveu um programa de computador que cria sudokus (o processo de bolar um puzzle do zero, como você verá a seguir, é trabalhoso). Em 2004, o jornal britânico The Times passou a publicá-los regularmente, e logo foi seguido por outros periódicos. O puzzle voltava ao ocidente com seu nome oriental.
Howard Garns morreu em 1989, sem ver seu jogo explodir ao redor do mundo. Não é exagero, aliás, dizer que o sudoku virou uma febre, principalmente no Reino Unido: o britânico The Guardian chegou a ter uma seção do jornal com jogos de sudoku em todas as páginas, e a TV BBC de Londres transmitiu quatro temporadas de um game show de sudoku, chamado Sudo-Q. A ideia de que o jogo seria um “exercício para o cérebro” ajudou a impulsionar a popularidade. Também vale notar que a ascensão aconteceu na era pré-smartphone – quando havia mais demanda para passatempos que distraíam a cabeça no ônibus ou na sala de espera do dentista.
O puzzle já não tem o mesmo alcance, claro. Mas também não é irrelevante. Está entre os cinco aplicativos mais baixados da categoria “jogos de tabuleiro” na App Store, à frente do xadrez. Faz todo sentido, visto que as regras do sudoku são tão simples que podem ser escritas em cinco linhas: o jogador deve completar cada quadradinho com um número de 1 a 9, sendo que não pode haver números repetidos dentro das mesmas linhas, colunas e nos blocos 3 × 3 em negrito (para facilitar, vamos chamá-los apenas de “blocos”, enquanto os quadradinhos em que vão os números serão “células”).
O sudoku também contém dicas: números fixos espalhados pelo quadriculado, por onde o jogador deve começar a resolver. Sem elas, os números poderiam ser organizados de várias maneiras diferentes pelo tabuleiro. Ou seja: são elas, as dicas, que conferem uma única solução possível para cada partida de sudoku.
O jogador sequer precisa de matemática para resolver o puzzle: os números poderiam ser substituídos por letras ou emojis, sem impacto algum na resolução. Mas o jogo também suscita problemas matemáticos.
Todo sudoku é um “quadrado latino”, conceito estudado amplamente pelo matemático Leonhard Euler nos anos 1770. Em análise combinatória, um quadrado latino é um quadriculado (“matriz”, no termo matemático) de n colunas e n linhas com símbolos que ocorrem apenas uma vez em cada uma. Euler usava letras do nosso alfabeto (o latino) como símbolos, daí o nome.
O sudoku, então, é um quadrado latino de matriz 9 x 9 – com o adicional de que seus blocos internos de 3 × 3 também não repetem símbolos (por exemplo, não rola um número 2 no quadradinho diagonal a outro 2). Isso confere algumas características interessantes ao quebra-cabeça, que veremos a seguir.
A lógica por trás do Sudoku
Quantas soluções diferentes existem para o sudoku? Euler também queria saber – só que para os quadrados latinos. Não conseguiu. O matemático chegou a calcular o valor para matrizes menores, mas não encontrou uma fórmula ou método que valesse para todos os tamanhos.
Sem computadores, não teria jeito. O número total de matrizes 9 x 9 diferentes só foi calculado em 1975: existem 6 × 1027 maneiras de organizar os números nas células, sem repeti-los em nenhuma linha ou coluna (1). Adicionando a regra extra do sudoku, de não permitir repetições nos blocos 3 × 3, o número cai para 6,7 x 1021 – ou, mais precisamente, 6.670.903.752.021.072.936.960.
São 6,7 sextilhões de possibilidades. É mais do que o número de grãos de areia na Terra (7,5 x 1018) e chega perto do número de estrelas do universo conhecido (10 x 1021). Mas muitas dessas soluções de sudoku são bem parecidas entre si, graças à simetria das matrizes.
Suponha que você tenha um sudoku completo em mãos. Se rotacionar todos os números da tabela para a direita, esquerda ou virá-los de cabeça para baixo, você gera três novas soluções válidas. O mesmo acontece se você espelhar a matriz no eixo horizontal, vertical e nos dois eixos diagonais.
Outro truque: se trocar os números da primeira linha com os da segunda ou da terceira, você também obtém resultados válidos. Basta que essas linhas estejam no mesmo bloco (caso contrário, números iguais poderiam cair juntos, quebrando a regra do jogo). O mesmo vale para colunas.
Por fim, ainda dá para trocar só os números de lugar: colocar todos os 1 no lugar dos 2, os 6 no lugar dos 7 e por aí vai. Juntando essas estratégias, dá para fazer milhões de matrizes diferentes a partir de uma só – o que é uma mão na roda para os autores de sudoku.
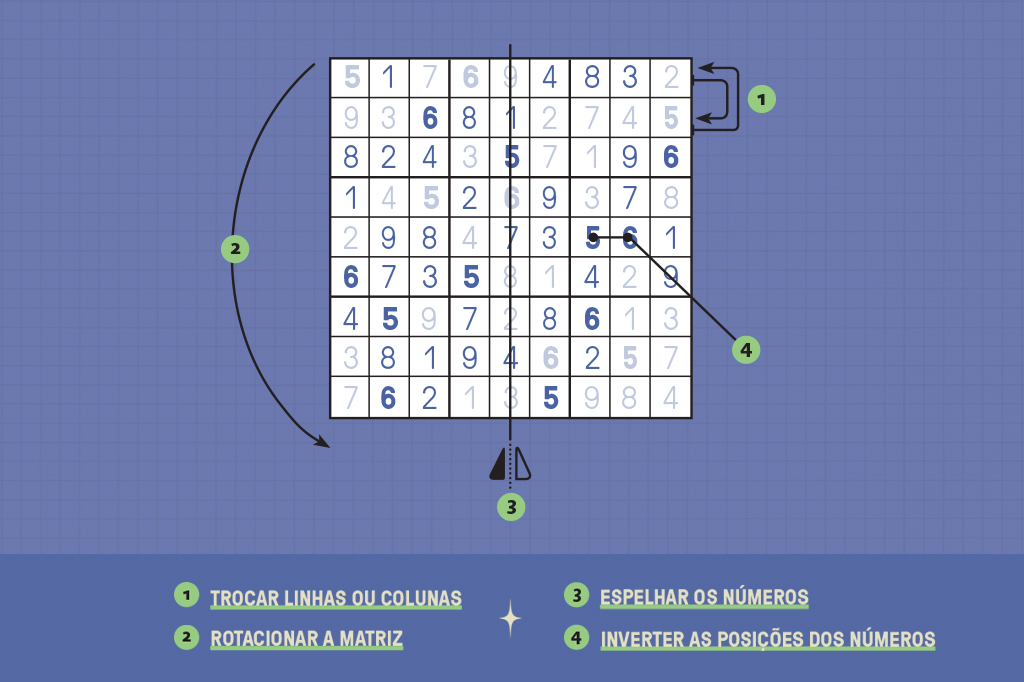
Antes daquele software neozelandês do começo dos anos 2000, os sudokus eram feitos à mão: o autor começa preenchendo uma matriz vazia com números, seguindo as regras do jogo. Quando estivesse com a matriz completa (ou seja, a resolução de um puzzle), poderia usar as propriedades simétricas para gerar outras resoluções sem quebrar tanto a cabeça.
Daí vem a parte difícil. O autor começa a apagar alguns dos números – esses serão os que você vai ter de descobrir na hora de jogar. Os que sobrarem vão ser as dicas, ou seja, aqueles que já vêm impressos.
Mas a cada um ou dois números deletados, é importante verificar se o sudoku ainda é válido – se ele continua com apenas uma solução possível. Para facilitar a visualização: sem dica nenhuma, seriam 6,7 sextilhões de soluções; deixando uma, duas, três… a quantidade vai diminuindo. Até que uma hora chega um número mágico de dicas – aquele a partir do qual é possível montar um sudoku com uma única solução possível (mais sobre isso daqui a pouco).
Bom, no meio do caminho, é possível que o criador do puzzle acabe apagando um “número inevitável”: uma célula que, se estiver em branco, deixa o sudoku com duas (ou mais) soluções possíveis. Aí ele tem de voltar atrás: aquele número precisa ser uma das dicas.
Hora de resolver. A estratégia mais simples envolve passar os olhos pelo puzzle e verificar se há alguma célula que só permite um único número. Ou, então, encontrar o único quadrado em que determinado número se encaixa. Os sudokus de nível fácil podem ser resolvidos usando apenas esse raciocínio.
Mas as técnicas vão ficando mais sofisticadas à medida que a dificuldade aumenta, daí é necessário um lápis para anotar os possíveis números que vão em cada quadradinho. Você pode identificar duas células que comportam apenas os mesmos dois números (exemplo: em uma célula só cabe 1 e 9, e na outra também). Nesse caso, aqueles números precisam estar ali, e qualquer possibilidade de encaixá-los em outras células pode ser excluída. A mesma lógica vale para trios de números.
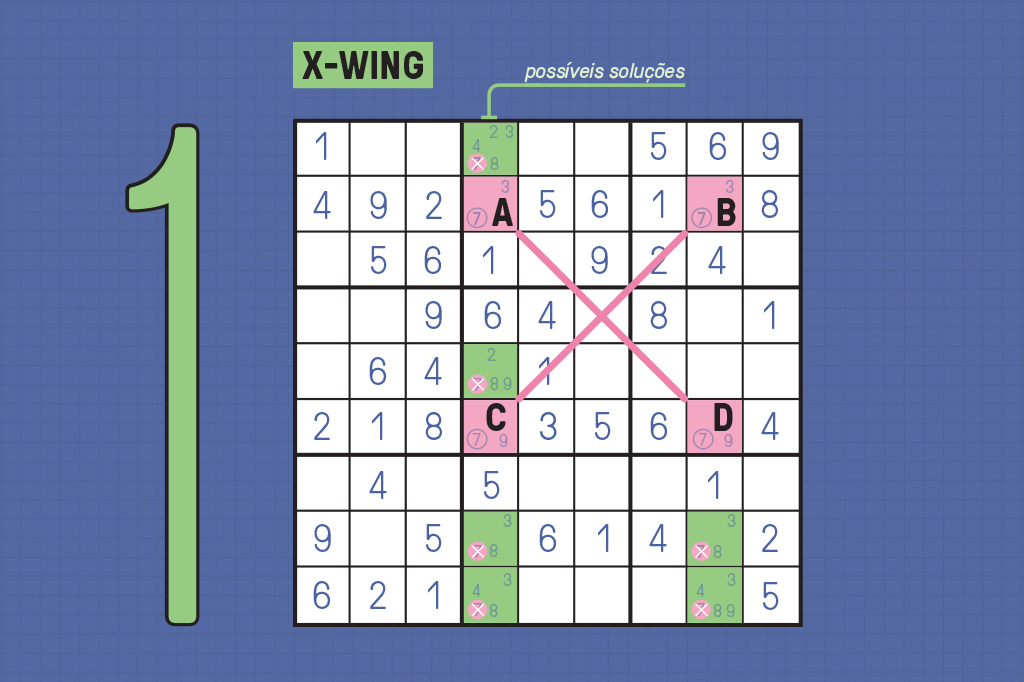
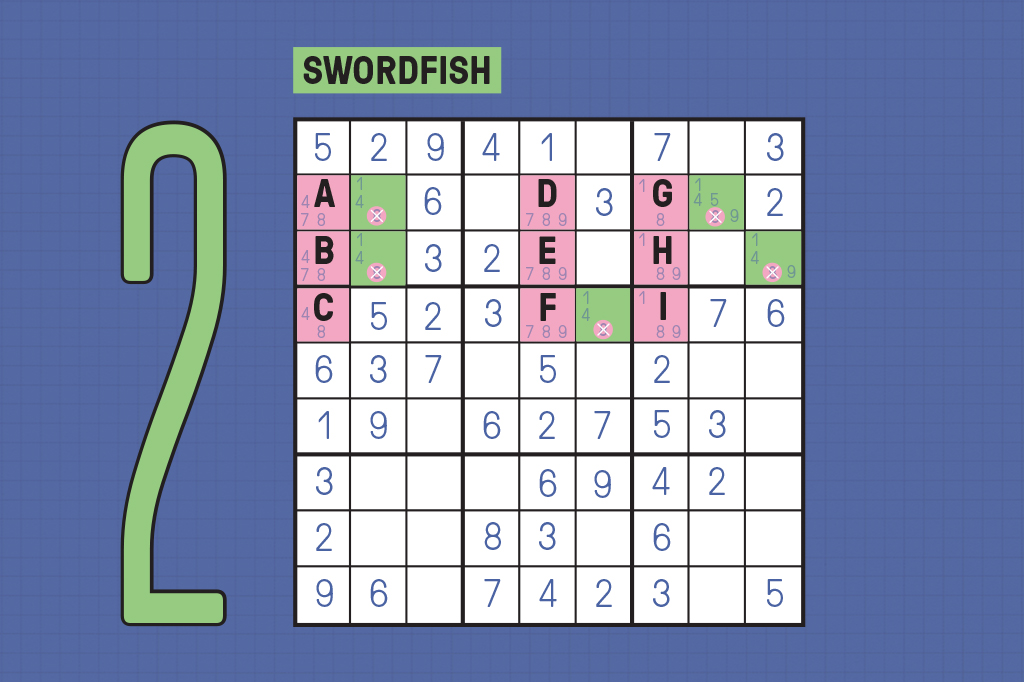
Outras estratégias ganham nomes atraentes, como swordfish (peixe-espada) e x-wing (o nome de uma nave de Star Wars) – veja como aplicá-las no infográfico abaixo. Mas a verdade é que, com muita prática, você pode deduzi-las usando apenas a lógica.
O número de dicas geralmente define a dificuldade de um puzzle. Um sudoku de nível fácil pode ter 38 dicas, enquanto o expert tem 22. O que nos leva à segunda questão matemática: qual é o menor número de dicas que um sudoku pode ter para que ele continue tendo uma única solução?
O problema da década
“Quem resolver essa questão será um rockstar no universo de pessoas que ligam para sudoku. É bem menor do que o universo de pessoas que ligam para rockstars de verdade – mesmo assim, seria bacana.”
É assim que o livro Taking Sudoku Seriously (“Levando o Sudoku a Sério”), de 2011, descreve o problema. Na época, alguns grupos de pesquisa tentaram – sem sucesso – provar matematicamente qual seria o menor número de dicas possível para um sudoku de solução única (2).
O matemático australiano Gordon Royle chegou a reunir 50 mil puzzles de solução única que forneciam apenas 17 dicas. Mas nunca encontrou o mesmo para números menores. Todo sudoku de 16 dicas que ele verificava permitia pelo menos duas soluções diferentes. Ou seja: existiam pelo menos duas matrizes distintas que poderiam se encaixar naquelas 16 dicas. Como se fosse uma questão do Enem com mais de uma alternativa certa.
Bom, isso por si só já era uma pista de que não há soluções únicas com 16 dicas ou menos. Só que, para provar essa hipótese, seria necessário verificar todos os sudokus possíveis de 16 dicas, e ver se algum deles comporta apenas uma solução.
Isso significa encontrar todas formas possíveis de selecionar 16 números dentro de uma matriz (são 3,3 x 1016 formas) e testar todas as matrizes possíveis (lembrando: 6,7 x 1021) para cada uma dessas configurações. O objetivo é verificar se mais de uma matriz se encaixa como solução em cada seleção de 16 números.
É impraticável checar esse tanto de puzzles. Um computador demoraria 300 mil anos para fazer a conta. Alguém teria de achar uma forma de contornar o problema, ou o pequeno universo de nerds de sudoku morreria sem saber a resposta.
O rockstar em questão surgiu em 2012, um ano depois do livro que citamos aqui. Foi o matemático Gary McGuire, da Universidade de Dublin. Em conjunto com outros programadores, ele encontrou uma forma de provar que o menor número de dicas possível para que o sudoku tenha uma única solução é, mesmo, 17.
“Tínhamos de encontrar saídas matemáticas para reduzir o tempo de computação”, diz Gary. “É sobre a diferença entre o que é possível e o que é impossível.”
O truque foi usar a simetria intrínseca ao sudoku. Caso uma determinada matriz tenha uma única solução para 16 dicas, então as matrizes simétricas a ela também terão. Dessa forma, não precisamos usar todas elas na conta. Em vez de 6,7 x 1021, o computador pode checar “só” 5,5 x 109 sudokus.
Isso já reduz o tempo de processamento drasticamente. Além disso, a equipe programou um algoritmo para encontrar os “números inevitáveis” de cada um desses sudokus. Assim, não precisariam checar todas as combinações de 16 números, mas só aquelas que realmente poderiam levar a uma solução única.
Os pesquisadores usaram um supercomputador para checar esse número menor de puzzles. O processamento começou em janeiro de 2011 e terminou em dezembro do mesmo ano. O computador encontrou mais de uma solução para todos os sudokus de 16 dicas. O resultado foi publicado em um paper no mês seguinte (2).
Mais grupos de pesquisa confirmaram o cômputo. “Eu queria resolver esse problema antes de morrer. Foi uma sensação fantástica”, diz Gary. Posteriormente, o algoritmo desenvolvido pela equipe também foi avaliado para uso em biologia computacional e outras aplicações que envolvem destrinchar questões complexas (3).
O campeonato mundial
32 países fazem parte da Federação Mundial de Puzzles (World Puzzle Federation ou WPF). Ela foi criada por Will Shortz, editor de palavras cruzadas do The New York Times e celebridade do universo dos passatempos. Atualmente, a principal função da WPF é organizar o campeonato mundial de puzzles e o de sudoku.
O de puzzles rola desde 1992, com categorias individuais e em grupo. A competição é dividida em várias etapas, incluindo problemas de lógica inéditos e clássicos, como batalha naval, nonograma e o próprio sudoku.
O Brasil não só é um país membro do WPF como já sediou um campeonato mundial. A editora Ediouro, que publica a revista de passatempos Coquetel, foi a representante do Brasil no início dos anos 2000. Em 2007, organizaram o 16º Campeonato Mundial de Puzzles no Hotel Intercontinental, Rio de Janeiro. Qualquer pessoa interessada em participar poderia se inscrever por meio de um teste rápido no site da revista. Depois, a editora organizou três seleções nacionais para definir quem seriam os quatro membros do time brasileiro.
Ricardo Daniel Kossatz foi um membro convidado pela Coquetel a participar da edição brasileira. Ele fazia parte de um grupo de desafios de lógica na Mensa Brasil – uma sociedade que reúne pessoas de alto QI – e já havia participado dos mundiais de 2005 e 2006. A World Puzzle Federation enviou materiais para treinamento das equipes, aos quais ele se dedicava diariamente. Os participantes trocavam ideias sobre técnicas para melhorar o tempo de resolução e caminhos lógicos possíveis para cada puzzle.
A dica que Kossatz dá para diminuir o tempo de resolução do sudoku é criar “pontos de controle”: “São marcações que podem ser feitas no desafio, indicando que naquele ponto ficamos em dúvida sobre qual caminho seguir”, diz ele. Por exemplo: se há dois números possíveis em uma célula, vale escolher um deles e marcá-lo como ponto de controle. “Às vezes, a definição do caminho correto leva muito mais tempo do que escolher um ao acaso e seguir por ele até encontrar um erro – e, então, voltar ao ponto de controle para seguir por outro caminho.”
O sudoku sempre foi um dos puzzles mais esperados da competição. Tanto que, em 2006, surgiu o primeiro campeonato mundial de sudoku, na cidade de Lucca, Itália (infelizmente, o Brasil nunca participou de um desses). Além do jogo clássico, os participantes também devem resolver variações do puzzle, que adicionam mais regras ao desafio original.
No killer sudoku, por exemplo, o jogador deve posicionar os números de forma que a soma deles resulte em valores especificados nos quadradinhos. No sudoku X, as diagonais também devem conter números distintos. E no greater than sudoku, as células têm sinais que indicam se o número posicionado deve ser maior ou menor que aqueles ao redor. Essas regras extras permitem que o sudoku comece com menos de 17 dicas, e continue tendo uma única solução.
“Como tudo na vida, existem os mortais, como eu, mas também existem os deuses do Olimpo, com uma capacidade de raciocínio lógico tão privilegiada que dá gosto de vê-los resolvendo puzzles ao vivo”, lembra Kossatz. Exemplo disso é a jovem chinesa que detém o recorde de resolução mais rápida de sudoku. Com 14 anos, Wang Shiyao resolveu uma matriz de 27 dicas em 54 segundos. O recorde foi estabelecido na 13ª edição do campeonato, em 2018. Veja abaixo.
Sudoku é um passatempo – e como o nome diz, serve para preencher as horas, sem nenhuma função prática. Mas fez mais do que isso para a área da computação e para Ricardo, que se tornou produtor de conteúdo para a Coquetel e chegou a publicar puzzles aqui na Super.
Então, fica a dica. Numa época em que quase todo o tempo livre é gasto no Instagram ou no TikTok, vale dar uma chance ao mundo analógico. A rotina de passar de vídeo em vídeo em um feed infinito nem se compara à satisfação de resolver um bom puzzle.
Referências: (1) Artigo “The number of 9 × 9 latin squares”; (2) Artigo “There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem”; (3) Artigo “The minimal hitting set generation problem: algorithms and computation”.
Fontes: Departamento de matemática da Universidade Cornell; Daniel Lavouras, professor da educação básica e fundador de olimpíadas do conhecimento.
Os gatos fazem bem para a nossa saúde? Veja o que diz a ciência
Estes são os 100 nomes de bebês mais populares de 2017
Cientistas descobrem estratégia usada por orcas para caçar tubarões baleia
Como foi o acidente que matou Ayrton Senna?
Cientistas finalmente resolvem mistério dos gatos laranjas
ACESSO LIVRE COM VIVO FIBRA