Biólogo resolve problema matemático sem solução há 68 anos
Aubrey de Grey, professor de Cambridge, resolvia problemas de lógica no tempo livre – e acabou sendo mais rápido que os matemáticos profissionais
Por
SEGUIR
SEGUINDO
4 Maio 2018, 18h52 | Atualizado em 2 jul 2026, 17h17
Gosta de sudoku? De teste de QI? De aula de matemática? Então essa é para você, caro leitor herdeiro de Einstein: imagine um monte de pontos ligados por linhas do mesmo tamanho. O número de pontos não faz diferença. Podem ser quatro, cinco, seis, infinitos etc. O que é realmente essencial, só para reforçar, é que todas as linhas sejam idênticas. Assim (o exemplo da direita está errado, naturalmente):
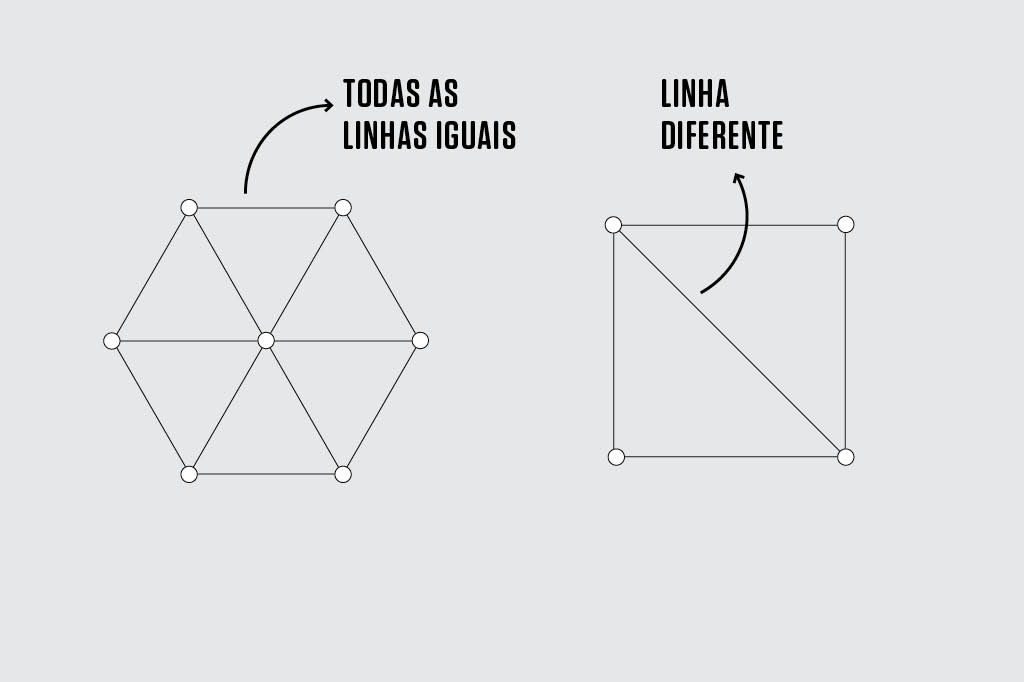
Sua missão, agora, é colorir os pontos. Mas não de qualquer jeito. Um ponto nunca, jamais, em hipótese alguma, pode ter a mesma cor dos pontos vizinhos. Se você pintar um ponto de vermelho, por exemplo, nenhum dos pontos a que ele estiver ligado poderá ser vermelho também. Ainda usando o hexágono de exemplo:
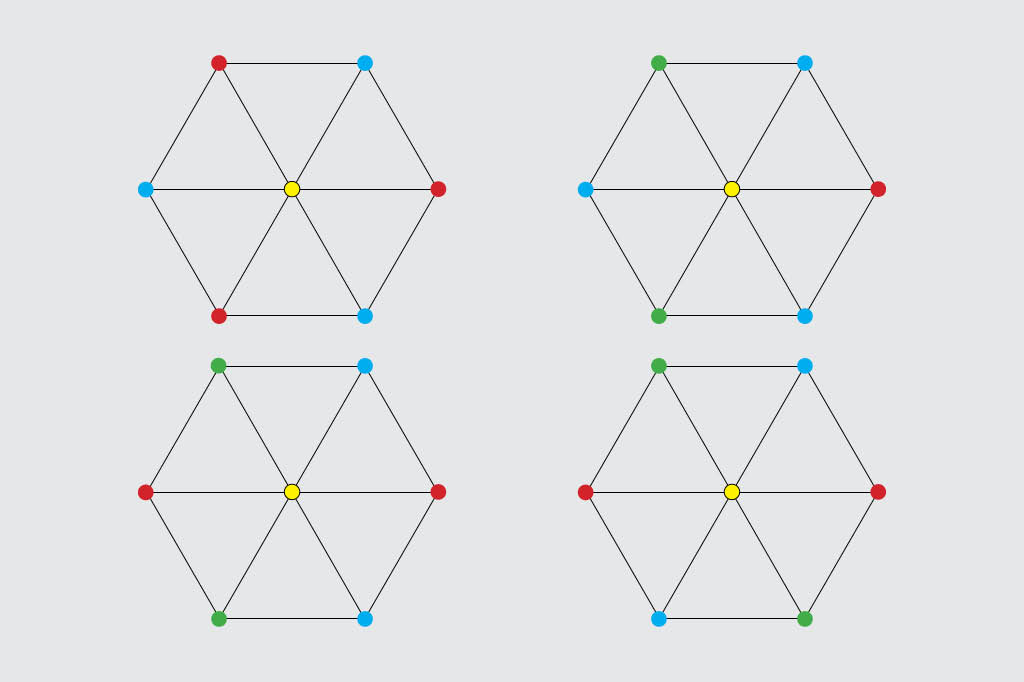
Legal, há algumas soluções possíveis. Com três cores dá para resolver. Com quatro fica bacana, também. Mas a questão é: qual é o mínimo de cores que você precisa para resolver qualquer conjunto de pontos? Qualquer um mesmo: oito, 140 mil, 2 milhões… em qualquer uma das incontáveis configurações possíveis.
Bem, aí a chapa esquenta: o problema foi proposto pelo americano Edward Nelson em 1950 – na época, estudante da Universidade de Chicago –, e desde então não havia recebido nenhuma resposta satisfatória. Já se sabe desde aquela época que esse número mágico é alguma coisa entre 4 e 7, mas a resposta definitiva ainda é um mistério. Ou era.
Quem acaba de dar um passo importante para salvar a pátria é o biólogo britânico (muito) barbudo Aubrey de Grey – que não, não é formado nem pós-graduado em matemática. Brincando com o problema no seu tempo livre, o professor de Cambridge descobriu uma exótica configuração de pontos e linhas que não pode ser resolvida com menos de cinco cores. Foi o primeiro avanço na busca de uma solução para o problema em 68 anos. Agora, a janela de 4 a 7 foi reduzida para 5 a 7.
A façanha – relatada neste artigo científico – só foi possível graças a um monstro geométrico de 20,4 mil vértices, construído a partir da combinação de formas de onze vértices iguais a que você vê aqui embaixo. Criadas pelos irmãos Leo e William Moser, essas figuras são especiais porque, apesar da simplicidade aparente, precisam obrigatoriamente de quatro cores para dar certo. Isso as torna um ótimo ponto de partida para bolar um jogo de pontos que exija ainda mais cores.
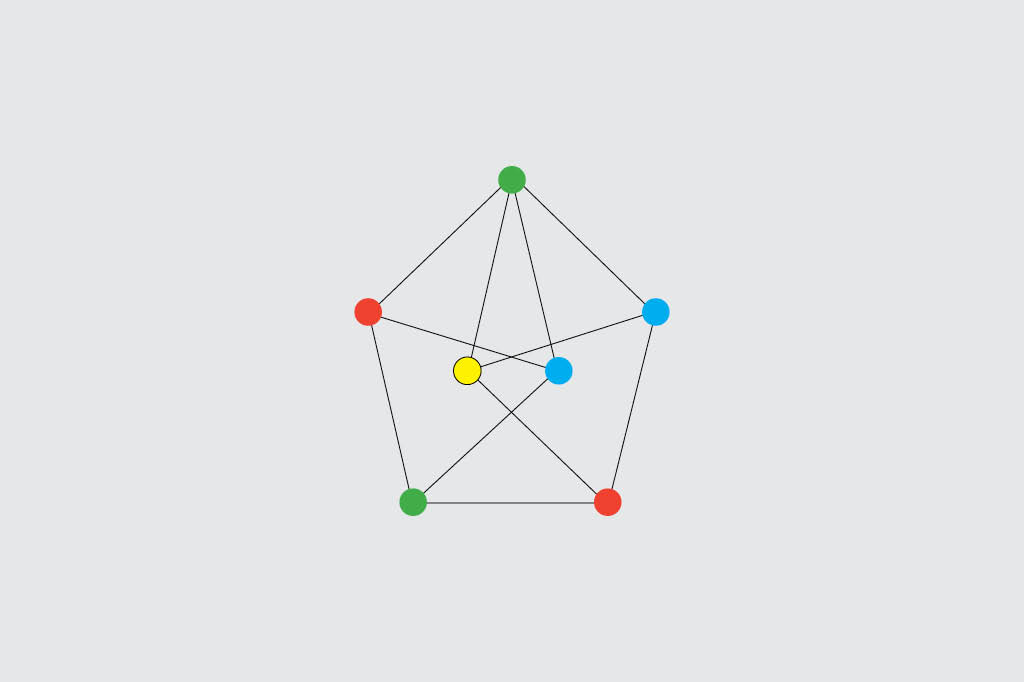
Parece uma questão completamente desligada da realidade, mas não é: imagine um mapa-múndi político, em que cada país é de uma cor. Nenhum dos 14 países que faz fronteira com a China, por exemplo, pode ser da mesma cor que ela. De quantas cores você precisa? Bingo.
Não é a primeira vez que um amador passa a perna em matemáticos profissionais. Notícias como essa são sempre recebidas com entusiasmo no meio. “Eu brinquei com problemas matemáticos que estão em aberto por toda a minha vida adulta”, afirmou de Grey ao The Guardian. “Mas essa é a primeira vez que eu faço um avanço, e eu já tenho 55 anos! Provavelmente será a primeira e a última.” Aubrey de Grey já era famoso antes disso, mas por outro motivo: sua alegação excêntrica de que os primeiros seres humanos que vão chegar aos mil anos de idade já nasceram – e que um deles pode ser você. Veja a entrevista dele na SUPER.
ACESSO LIVRE COM VIVO FIBRA